

Aust J Crop Sci. 19(04):369-377 (2025) | ISSN:1835-2707
https://doi.org/10.21475/ajcs.25.19.04.p257
Influence of drying process variables on hot air convection drying characteristics of pale flesh white skin sweet potatoes (Ipomoea batatas)
Aboubakar Compaore1,2*, Salifou Ouedraogo3, Honoré Kondia Ouoba3, Fayçal Ilboudo3, Bétaboalé Naon3
1Université Lédéa Bernard OUEDRAOGO (Ex Université de Ouahigouya), 01 BP 346 Ouahigouya 01, Région du Nord, Burkina Faso
2Laboratoire de Physique et de Chimie de l’Environnement (LPCE), Ecole Doctorale Sciences et Technologie (ED-ST), Université Joseph KI-ZERBO, Ouagadougou, Burkina Faso
3Laboratoire de Matériaux de l’Héliophysique et Environnement (La.M.H.E.), Unité de Formation et de Recherche en Sciences Exactes et Appliquées (UFR/SEA), Université Nazi BONI, Bobo Dioulasso, BP 1091, Burkina Faso
*Corresponding author: Aboubakar Compaore

 ORCID number: https://orcid.org/0000-0002-1105-4210
ORCID number: https://orcid.org/0000-0002-1105-4210
Abstract: Drying of spherical sweet potatoes (Ipomoea batatas) with pale flesh and white skin (a newly introduced variety grown in Burkina Faso) was carried out at air temperatures of 50°C, 60°C, 70°C and 80°C using 2 and 3 cm diameter samples to study the influence of process variables including air temperature and sample diameter on drying characteristics. The results of the analyzed drying data indicated that moisture content was influenced by sample diameters and hot air-drying temperatures. Increasing air temperature and sample diameter resulted in reduced drying time for temperature influence and increased drying time for diameter influence. Effective moisture diffusivity decreased relatively with increasing moisture ratio value at all hot air temperatures. A polynomial of degree five was derived to correlate the effective moisture diffusivity with the moisture ratios of sweet potato spheres. The average effective moisture diffusivity increased as the air temperature and the diameter of the spherical sweet potato samples increased. The air temperature dependence of the average effective moisture diffusivity values was described by an Arrhenius-type equation. This dependence allowed the determination of the activation energy values of the spherical sweet potato. The activation energy values increased by 30.50 and 27.71 kJ/mol when the sample diameters varied from 2 to 3 cm.
Keywords: Activation energy; convective drying; moisture content; moisture diffusivity; sweet potato.
Introduction
Hot air convection drying is the process of removing water with air via simultaneous transfer of heat, mass and momentum. The food's need for heat is achieved by contact of the food with a flow of hot air. The energy transmitted to the surface of the food by convection of hot air is transferred inside the food by diffusion and/or convection, depending on the physical and biological structure of the food to be dried. This heat flow causes an increase in product temperature and evaporation of surface water. Moisture is transferred from the surface of the product to the air by convection in the form of water vapour and from the interior of the product by diffusion, convection or capillarity. The drying rate and characteristics of dried foods depend on the conditions of the air-drying process such as air temperature, relative humidity of the air, air velocity, orientation/ direction of air flow and vapour pressure in air. The drying rate also depends on the characteristics of the foods to be dried such as geometry, thickness/size, shape and physical/ biological configurations of the foods. The complexity of the physic-biological configurations of wet foods, the variety of transport phenomena and biological diversity make food drying a challenge (Doymaz et al., 2023). To address this challenge, many researchers have been interested in investigating various experimental processes of drying foods such as the tuberous roots category.
Sweet potato called scientific name Ipomoea batatas is a plant cultivated mainly for its edible tubers (tuberose roots), rich in starch. These tubers produced are designated by the same name as this plant. Sweet potatoes produce more edible energy on marginal lands than any other major food crop. In addition to this useful property, these tubers can resist unwanted abiotic and biotic stresses and do not require intensive care. They therefore play an important role in the economy of poor households where they constitute a major source of subsistence and are considered a food to combat famine and child malnutrition. Besides this important function, sweet potato cultivation has immense semi-industrial/industrial value for starch extraction and animal feed production. For all these explanations, sweet potato offers great possibilities for achieving food and nutritional security in developing and underdeveloped countries where most agricultural fields belong to vulnerable population categories (Amagloh et al., 2021). Sweet potatoes are important tubers rich in fibre, starch, vitamins, minerals and bioactive compounds. They contain essential carotenoid, phytochemical, anticancer and antimicrobial properties useful for human and animal health. Sweet potato raw or in its processed form can be consumed by humans as a staple food, snack or baked goods. However, sweet potato is susceptible to microbial activities which can lead to degradation and spoilage due to its high moisture content. Furthermore, sweet potato is seasonal and cannot maintain optimal quality level for a long period after harvest. Thus, it is often used shortly after harvest or preserved using the hot air convection drying method (Onwude et al., 2019). In the literature, several drying processes have been applied to different sweet potato varieties, namely, infrared and fluidized bed drying (Thao and Noomhorm, 2011), convective hot air drying (Adie and Inyang, 2024), microwave drying (Junqueira et al., 2022), hybrid microwave and hot air drying (Tüfekçi and Özkal, 2023), spouted bed drying (Rezende et al., 2024), sun and drum drying (Badiora et al., 2023), spray drying (Arebo et al., 2023), freeze-drying (Antal, 2023) and solar drying (Sakouvogui et al., 2023). Pretreatments before drying have been applied to sweet potatoes including steaming (Dinrifo, 2012), blanching with hot water and steam (Badiora et al., 2023), soaking in sodium metabisulfite solution (Edeani and Anyaene, 2023), osmotic dehydration with sucrose and sorbitol (Junqueira et al., 2022), immersion in citric acid solution (Antal, 2023), lemon juice and saline solution (Ayonga et al., 2023) and soaking in sodium metabisulfite solution (Shamala and Fouda, 2023). These drying and pretreatment techniques were applied on sweet potato samples with several sliced shapes, varieties, skin and flesh colours including sweet potato cubes (Singh and Pandey, 2012), white skin and yellow-red flesh sweet potato slices of Kratai cultivar (Thao and Noomhorm, 2011), strips (Obregon et al., 2020), chips (Souza et al., 2019), Nigerian variety slices (Olawale and Omole, 2012), and Chinese local variety slices (Fan et al., 2015). It was found that there are few papers on air drying of spherical sweet potato in this literature. The objective of this paper is to investigate the influence of drying variables namely air temperature, sample diameter and moisture ratio on the drying characteristics e.g. moisture diffusivity of white skinned and pale fleshed spherical sweet potato, a newly introduced variety cultivated in Burkina Faso. This study will contribute to improve the physical understanding of the drying behaviour of the spherical shape of this sweet potato variety.
Results And Discussion
Influence of drying air temperature on moisture ratios
The spherical sweet potato samples with initial diameters of d = 2 cm and d = 3 cm were dried at hot air temperature levels (50, 60, 70 and 80 °C). The initial moisture contents of the spherical sweet potato samples were observed to be 2.2305 (d.b.), 3.0233 (d.b.), 3.4258 (d.b.) and 3.3898 (d.b.) at air drying temperatures of 50 °C, 60 °C, 70 °C and 80 °C for 2 cm diameter samples, respectively. For 3 cm diameter spherical samples, the initial moisture contents were 2.5564 (d.b.), 2.9792 (d.b.), 3.6894 (d.b.) and 2.7938 (d.b.) at air drying temperatures of 50°C, 60°C, 70°C and 80°C, respectively. These values indicated that these were perishable root tubers with large amounts of water that could cause their deterioration. Then, during hot air drying, the moisture contents were reduced to 0.0878 (d.b.), 0.0852 (d.b.), 0.0825 (d.b.) and 0.0796 (d.b.) at drying air temperatures of 50°C, 60°C, 70°C and 80°C, respectively, for 2 cm diameter spherical samples. For 3 cm diameter spherical samples, their moisture contents were reduced to 0.0878 (d.b.), 0.0852 (d.b.), 0.1137 (d.b.) and 0.0822 (d.b.) at drying air temperatures of 50°C, 60°C, 70°C and 80°C, respectively. From the curves, it can be inferred that the sweet potatoes were completely dried for 2000, 1376, 840 and 580 minutes at 50°C, 60°C, 70°C and 80°C respectively for the 2 cm diameter spherical samples (Figure 1a). For the 3 cm diameter samples, the drying times were found to be 2080, 1600, 1419 and 915 minutes at 50°C, 60°C, 70°C and 80°C respectively (Figure 1b). Therefore, the moisture content of the spherical sweet potato samples decreased to a constant point in a time that depends on the air-drying temperature and the diameter of the spherical samples, with the lowest time being at 80 °C (i.e. 580 minutes) and the highest time at 50 °C (i.e. 2000 minutes) during the drying of the 2 cm diameter spherical samples. For the 3 cm diameter spherical samples, the lowest time at 80 °C was 915 minutes and the highest time at 50 °C was 2080 minutes. Thus, an increase in air temperature results in a reduction in drying time. Some research has been conducted on the influence of air temperature on the moisture content of drying products. Gazor and Minaei (2005) reported that the drying time of pistachios was reduced with increasing inlet air temperature. Increasing the temperature from 60 to 90 °C reduced the drying time by about 35–40%. This was probably due to the rapid drying and surface shrinkage at high temperatures. The shrinkage of pistachio surfaces resulted in lower porosity on these surfaces, thereby reducing the moisture evaporation rate (Gazor and Minaei, 2005). Doymaz (2011) found that, when drying eggplant, drying was a thermally activated process. As the temperature increased, the initial slope of the drying curve increased and the drying time required to reach the final moisture content decreased accordingly (Doymaz et al., 2023). Abano et al. (2011) studied the drying of tomato slices and reported that increasing the temperature accelerated the drying process. As the hot air temperature increased, moisture removal also
Table 1. Regression coefficients of effective moisture diffusivities for sweet potato spheres at different drying conditions.
| Diameter (cm) | Temperature (°C) | Regression coefficients | R2 | |||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | |||
| 2 | 50 | 2.3880×10-7 | -5.3611 | 3.4657×10-7 | 3.1271×10-9 | -6.5565×10-8 | 1.5418×10-8 | 0.9989 |
| 60 | -8.8915×10-8 | 3.6908×10-7 | -5.8807×10-7 | 4.4908×10-7 | -1.6187×10-7 | 2.2745×10-8 | 0.9995 | |
| 70 | -4.3340×10-9 | -1.8792×10-8 | 2.6642×10-8 | 2.4926×10-8 | -3.8949×10-8 | 1.3095×10-8 | 0.9933 | |
| 80 | -2.7831×10-8 | 5.1882×10-8 | -3.9250×10-8 | 3.6617×10-8 | -2.8173×10-8 | 1.0268×10-8 | 0.9911 | |
| 3 | 50 | 3.4760×10-7 | 1.1745×10-6 | -1.5425×10-6 | 9.7919×10-7 | -2.9628×10-7 | 3.4586×10-8 | 0.9995 |
| 60 | -5.4561×10-7 | 1.7740×10-6 | -2.2509×10-6 | 1.3899×10-6 | -4.1274×10-7 | 4.7698×10-8 | 0.9995 | |
| 70 | -4.8764×10-7 | 1.6557×10-6 | -2.2008×10-6 | 1.4223×10-6 | -4.3907×10-7 | 5.2221×10-8 | 0.9996 | |
| 80 | -1.5039×10-8 | 3.6759×10-7 | -9.4571×10-7 | 9.3179×10-7 | -3.9349×10-7 | 6.1827×10-8 | 0.9994 | |
Table 2. Mean effective humidity diffusivity values calculated at air temperatures of 50°C to 80°C for hot air drying of spherical sweet potato samples of (2 and 3 cm) diameter.
| Temperature (°C) | Average effective moisture diffusivity (m2/s) | |
|---|---|---|
| Diameter: 2 cm | Diameter: 3 cm | |
| 50 | 1.4086×10-9 | 2.6715×10-9 |
| 60 | 2.3191×10-9 | 3.8326×10-9 |
| 70 | 3.0792×10-9 | 4.2045×10-9 |
| 80 | 3.7214×10-9 | 6.8775×10-9 |
Table 3. Values of activation energy and pre-exponential factor.
| Parameters | Activation energy (Ea) and pre-exponential factor (D0) | |
|---|---|---|
| Diameter: 2 cm | Diameter: 3 cm | |
| D0 | 12.887×10-5 | 7.9999×10-5 |
| Ea | 3.0502 ×104 | 2.7711×104 |
| R2 | 0.9644 | 0.9362 |
increased and ultimately resulted in a reduction in drying time (Abano et al., 2011).
Influence of sample diameter on moisture ratio
The size of the spherical sample diameters had a significant influence on the moisture ratio, as shown in Figure 2. Figure 2 presents the moisture ratio according to the drying time of spherical sweet potato samples for two diameters (2 and 3 cm) dried at a hot air temperature of 50 °C. From this figure, we note that the reduction of the sample diameter resulted in a reduction in the drying time. Thus, spherical sweet potato samples with a diameter of 3 cm spend more time than samples with a diameter of 2 cm, as presented in Figure 1 and Figure 2. For other drying air temperatures, when the diameter of the spherical samples increased, the drying time was also prolonged. An explanation for this result could be due to the increase in the distance travelled by liquid water/vapor and the increase in the surface area of the spherical sample in contact with the hot air. Our results are consistent with the drying results on the effects of food material size from other researchers. Royen et al. (2020) obtained during convective drying of apple slices that the drying time required for 4 mm slices was 300 min while one working day (maximum 10 h) was not sufficient to dry 12 mm slices. The drying measurement was stopped after 8.5 h and was resumed the next day. The reason for the extension of the drying time was explained by the increase in the thickness of the drying slice (Royen et al., 2020). When drying intact and pickled onion slices, Sufer et al. (2017) found that an increase in onion slice thickness also resulted in an increase in drying time due to the increase in the path length for moisture transfer (Süfer et al., 2017). Bebartta et al. (2014)
reported that the slice thickness of the samples influenced the drying time during fluidized bed drying of onion shreds. Indeed, the drying time of onions cut into 2 mm and 6 mm thick slices was 1427 and 1858 min, respectively, at an air velocity of 1 m/s and an air temperature of 50 °C (Bebartta et al., 2014). Fan et al. (2015) dried sweet potato slices of thickness (0.3–0.8 cm) using hot air. At all drying air temperatures, drying time increased with sample thickness. This was due to the large distance travelled by water and the increased exposed surface area for a given volume of sweet potato samples (Fan et al., 2015).
Influence of moisture ratio on effective moisture diffusivity
The effective moisture diffusivity (Deff) is influenced by air temperature for all diameter sizes of sweet potato samples. The logarithms of the moisture content values are calculated against drying time at air temperatures of 50, 60, 70 and 80 °C. It is clear that the relationship is relatively non-linear in nature. The non-linearity of the curves indicates the variation of moisture diffusivity with moisture content of spherical sweet potatoes. The Fourier number was calculated using equation (11) to determine the Deff values of spherical sweet potato for diameters of 2 and 3 cm at warm air temperatures. The evolution of effective moisture diffusivity as a function of humidity content was illustrated in Figure 3 for 3 cm diameter samples at air temperatures of 50, 60, 70 and 80 °C. These representative curves were relatively similar to those for 2 cm diameter samples. We noticed that effective moisture diffusivity decreased with increasing humidity for all hot air temperatures. Similar results were observed for drying mushroom slices. The authors of this mushroom research found that as moisture content decreased, vapor permeability increased, provided that the pore structure was open (Darvishi et al., 2013). This decrease in Deff could be due to the rapid increase in sweet potato temperature during the initial drying period. Spherical sweet potato samples would exhibit a high loss factor at high moisture content during this period. This would increase the water vapor pressure inside the pores of this food during drying and also cause the opening of these pores due to water pressure. During the first drying period, diffusion of liquid water could be the main mass transfer mechanism in the sweet potato spheres. As the drying of spherical sweet potato progressed, water vapor diffusion could become predominant over the drying time (Pinheiro and Castro, 2023). Similar results have been reported for cocoa bean roasting (Domínguez-Pérez et al., 2019), microwave drying of pistachio kernels (Jahanbakhshi et al., 2020) and hot air drying of tomato slices.
A polynomial of degree five gave a correlation between the Deff and the MR of the sweet potato spheres and equation (1) gave its expression:
\[D_{eff} = \alpha(MR)^{5} + \beta(MR)^{4} + \gamma(MR)^{3} + \delta(MR)^{2} + \varepsilon(MR) + \zeta\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)\]
where Deff is the effective moisture diffusivity (m2/s); MR is the moisture ratio (-); and regression parameters 𝛼, 𝛽, 𝛾, 𝛿, 𝜀, 𝜁 and the coefficient of determination (R2) of hot air drying for these sweet potato spheres at air temperatures of 50, 60, 70 and 80°C is presented in Table 1. The high R2 values (0 .9911–0.9996) showed an acceptable good fit of the equation representing the variation of Deff with respect to MR for sweet potato of 2 and 3 spherical diameters.
Influence of air temperature and sample diameter on mean effective moisture diffusivity (Deff, mean)
The mean moisture diffusivity is calculated by taking the arithmetic mean of the estimated Deff values over the MR range of food drying. The Deff,mean values of spherical sweet potato samples are given in Table 2. These Deff, mean values were obtained in the range of 1.4086×10-9 to 3.7214 ×10-9 m2/s and 2.6715×10-9 to 6.8775× 10-9 m2/s for 2 cm diameter samples and 3 cm diameter samples respectively as the temperatures increased from 50 °C to 80 °C (Figure 4). It can be seen that the Deff,mean, values increase as the air temperature level and the diameter of the sweet potato samples increased. Large diameter and high air temperature lead to an increase in the mean effective moisture diffusivity due to a large mass transfer. This is also due to the long migration path of moisture from the interior to the surface of the sample as the diameter size increases. Furthermore, this can be attributed to the availability of more thermal energy required to activate the movement of moisture from the inner part of the sweet potato to its surface for drying to take place. Because water is weakly bound to the food matrix at high temperature. Water activity increases with increasing temperature, which leads to increased moisture diffusion. Similar results regarding the influence of drying parameters on Deff,mean under different drying conditions have been found in the literature (Anabel et al., 2018; Süfer et al., 2017). When air drying
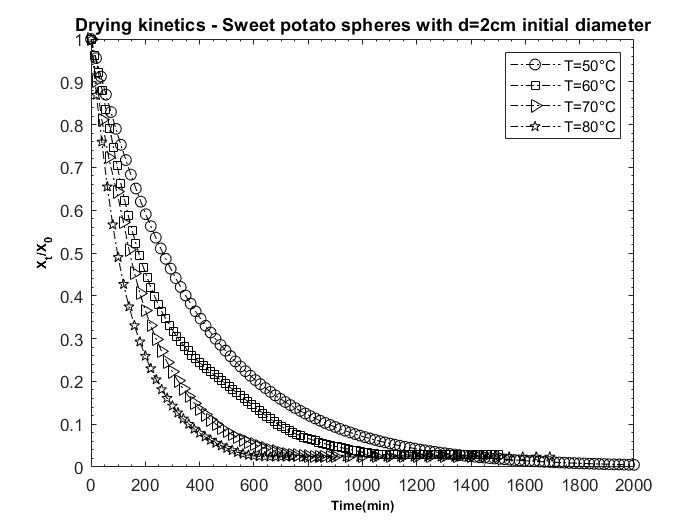
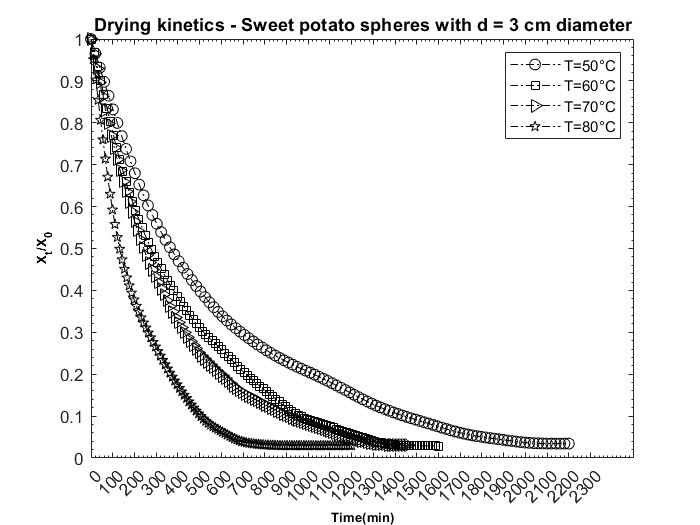
Figure 1. Drying kinetics of spherical sweet potato samples dried with hot air at temperature levels (50, 60, 70 and 80°C) with spherical samples of (a) d=2 cm and (b) d= 3 cm in diameter.
lemon slices, Torki-Harchegani et al. (2016) found that differences in the moisture diffusivity value of lemon during drying resulted from factors such as physicochemical properties and initial and final moisture contents. They also observed that the moisture diffusivity values of the food increased as the hot air temperature increased in the oven (Torki-Harchegani et al., 2016). Jiang et al. (2022) found that the moisture diffusivities of crabapple slices increased with thickness during its hot air drying (Jiang et al., 2022).
Influence of sample diameter on Activation Energy
Activation energy reflects the water retention potential of the food and the degree of difficulty in evaporating water. This index is determined by the moisture content and composition of the food itself. The higher the activation energy, the more difficult it is to remove moisture (Wang et al., 2022). The activation energy can be determined from the slope of the Arrhenius function, i.e., the natural logarithm of Deff,mean versus the reciprocal of the absolute
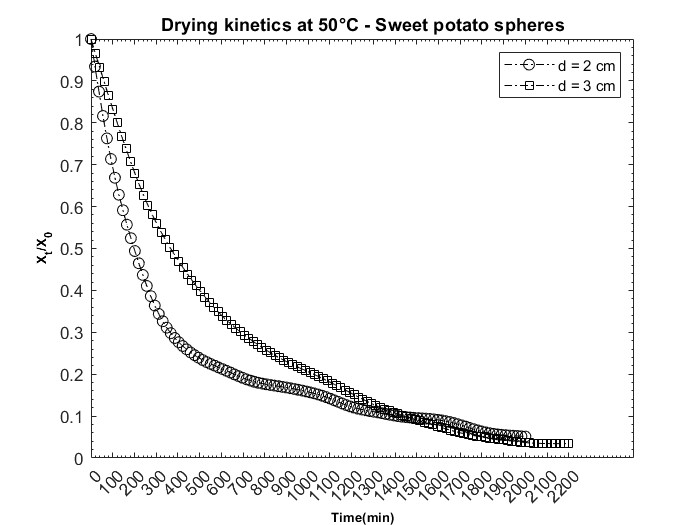
Figure 2. Moisture ratio versus drying time (min) of sweet potato spheres dried at 50°C air drying temperatures and at different diameters.
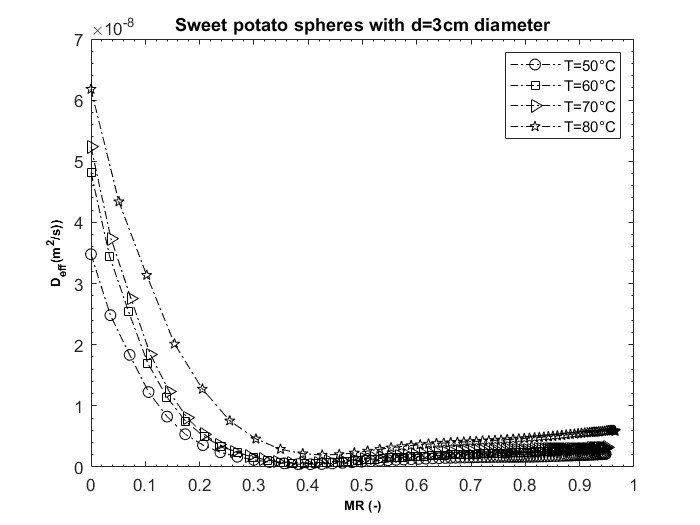
Figure 3. Variation of effective moisture diffusivity with moisture ratio for drying 3 diameter sweet potato spheres at 50°C, 60°C, 70°C, and 80°C air temperatures.
temperature of hot air for 2 and 3 cm diameter sweet potatoes. The results are given by Arrhenius-type models (Equation 2 and 3). Equations (2, 3) allow to express the values of Deff,mean according to the air temperature for sweet potatoes of 2 and 3 cm diameter:
For 2 cm diameter samples:
\[D_{eff,ave} = 12.887 \times 10^{- 5}\exp\left\lbrack - \frac{3.6686 \times 10^{3}}{T({^\circ}C) + 273.15} \right\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)\]
For 3 cm diameter samples:
\[D_{eff,ave} = 7.9999 \times 10^{- 5}\exp\left\lbrack - \frac{3.3329 \times 10^{3}}{T({^\circ}C) + 273.15} \right\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ (3)\]
The values of the activation energy for the samples of 2 and 3 cm diameter were respectively 30.50 and 27.71 kJ/mol (Table 3). The values of activation energy increase by 30.50 and 27.71 kJ/mol when the diameter of the samples varies from 2 to 3 cm. This variation of the activation energy with the diameter of the samples measures the high energy barrier in this food when the water migration path is long. This can be explained by the effect of the type, the composition, and the tissue characteristics of our drying product. Our influence results are consistent with other wet products under drying including crabapple slices (Jiang et al., 2022); African bean seeds (Igbozulike et al., 2023) and plantains (Kamble et al., 2022).
Materials and Methods
Sample preparation
Sweet potato was used as drying material in this study. Samples of the local variety of sweet potato with pale flesh and white-skinned, heavily consumed in low-income households, were purchased during the period of July 2023 at the market in the town of Bobo Dioulasso (Contact details: 11 ° 11′ 00″ North, 4° 17′ 00″ West), located in the Haut Bassin region of Burkina Faso. Sweet potato samples were transported and stored in refrigerated conditions (4 ± 0.5 °C) before the drying process at the laboratory of materials of Helio physics and environment of the Nazi BONI University from Nazi Boni University. Before drying, sweet potato samples were placed in laboratory to reach room temperature (25 ± 1 °C). Sweet potato samples were selected, washed, peeled, cut into spheres with diameters from 1 ± 0.002 cm to 3 ± 0.002 cm, measured manually using a digital calliper. This diameter range was suitable for the concept of thin-film drying tray. The sample diameter represented the thickness of the tray layer which is uniform and does not exceed 3 particle layers. In this case, it was assumed that the temperature distribution of the thin-film material was uniform (Onwude et al., 2016). Spherical samples are immersed in distilled water to remove excess surface starch film. Excess water on the spherical samples was removed using blotting paper and these sweet potato spheres were arranged in a single layer on a drying tray. The initial moisture content on a dry basis (d.b.) of sweet potato was determined using convective oven method at 105 ± 5 °C for 24 h (Compaoré et al., 2022). Triplicate samples were used for determination of moisture content and the average values were (3.0174±0.01) kgwater/kgdry matter.
Drying equipment
Drying experiments were carried out in an Air Performance laboratory oven (Froilabo, Model AC Standard Version, France, range 10–250°C with an accuracy of ±0.5°C) installed at the laboratory of materials of Helio physics and environment of the Nazi BONI University, Bobo-Dioulasso, Burkina Faso, previously described by Ouoba et al. (2021). Length, height and width of oven were 0.579 m, 0.640 m and 0.526 m respectively. Oven essentially consisted of a centrifugal fan to provide the desired drying air flow, a 1,000-Watt electric heater controlling the temperature of the drying air, an air filter and a proportional-integral-derivative controller (PID controller). Air temperature in convective oven was regulated to ±1∘C using a temperature controller. The oven operated at dry bulb temperatures of 10°C to 250°C. The desired drying air temperature was reached by an electric resistance and controlled by the heating control unit. The air speed was regulated by the centrifugal fan and a fan speed control unit. The air came out of the heating unit and was heated to the desired temperature, then channelled to the drying chamber through ventilation slots located in the rear side wall of the drying chamber. Fan located at the rear of chamber wall produced greater airflow and more intensive horizontal forced air circulation to dry the product samples. The samples were dried on a square perforated stainless-steel tray, having a flow cross section of 0.3 m x 0.3 m. The oven was adjusted to the selected air temperature for approximately 0.5 h before the start of the experiments to reach its steady state.
Drying procedure
Air drying temperatures were 50, 60, 70 and 80°C and air relative humidity was in range from 5 to 20%. Air velocity was kept at a constant value of 2.0 m/s with an accuracy of ±0.03 m/s for all drying experiments. Drying process began when drying conditions reached constant air temperatures. Once the oven reached stable conditions for set points, sweet potato samples were placed on a tray in a single layer and measurement started from that point. Experiments were carried out with 125 ± 0.3 g of sweet potato for all tests. Tray was removed from convective dryer regularly, at 20-minute intervals, and weighed with a digital electronic balance, then placed back in oven. The tray was removed from the dryer regularly, at 20-minute intervals, and weighed with a digital electronic balance, then placed back into the oven. The electronic digital balance (model 2102, Sartorius, France, range 0–2,100 g with an accuracy of ±0.001 g) was kept less than 1 m from the dryer (Wang et al., 2022). Convective hot air drying was continued until there was no longer any significant variation in the evolution of the masses of the spherical sweet potato samples. Drying tests were terminated when masses of samples were stabilized, which assumed that thermodynamic equilibrium was reached. The dried samples were cooled under laboratory conditions after each drying experiment and stored in airtight jars. The mass loss of the samples during drying was converted to moisture content on a dry basis and expressed as kgwater/kgdry matter according to equation (4). For each drying condition, averages of three replicates were taken as drying data. At end of each experiment, sample was heated in an oven at 105 °C for 24 h of drying to obtain the dry matter mass of this sample (Compaoré et al., 2022).
\[X(t) = \frac{m(t) - m_{s}}{m_{s}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)\]
Where X(t) is the moisture content on a dry basis (d.b.) expressed in kg water/kg dry matter; m (t), mass of spherical sweet potato samples, expressed in kg at time t in seconds and ms, mass of dry matter of spherical samples (kg).
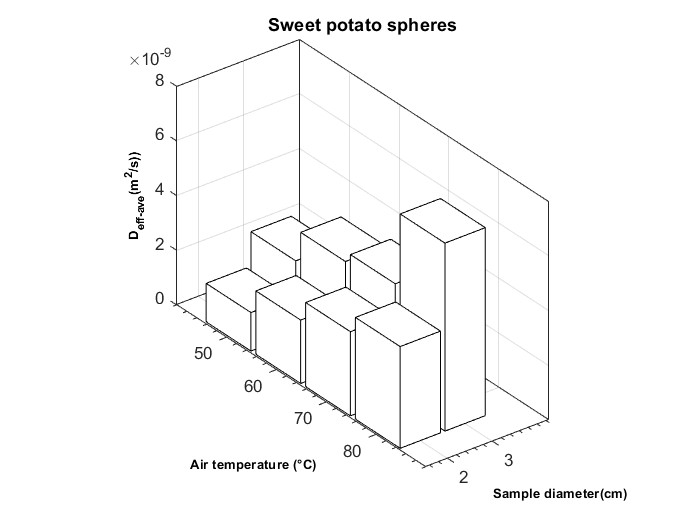
Figure 4. Variation of mean effective diffusivity with air temperature for 2 and 3 cm diameters.
Drying theory
Moisture ratio
Moisture ratio (MR) was calculated from moisture content data of spherical sweet potato samples during drying. Equation (5) was used to calculate the moisture ratio (Doymaz et al., 2023):
\[MR = \frac{X - X_{e}}{X_{0} - X_{e}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5)\]
Where X, X0 and Xe are respectively the average moisture content at any time of drying (kg water/kg dry matter) , the initial average moisture content (kg water/kg dry matter) and the equilibrium moisture content (kg water/kg dry matter).
As Xe is much smaller than X0 and X, it is negligible in this study. The moisture ratio then becomes:
\[MR = \frac{X}{X_{0}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6)\]
Effective moisture diffusivity
Drying of most food materials takes place during the falling rate period, and moisture transfer during drying process is controlled by internal diffusion. Fick's second diffusion equation (equation 7) was widely used to describe drying process during falling rate period of agricultural materials (Igbozulike et al., 2023):
\[\frac{\partial X}{\partial t} = D_{eff}\nabla^{2}X\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7)\]
Diffusion equation (equation 7) is solved for a sphere, assuming one-dimensional volume change of moisture movement, uniform temperature and constant mass diffusivity, and negligible external resistance (Igbozulike et al., 2023):
\[MR = \frac{6}{\pi^{2}}\sum_{n = 1}^{\infty}\frac{1}{(2n - 1)^{2}}\exp\left\lbrack - (2n - 1)^{2}\frac{{\pi^{2}D}_{eff}}{4r^{2}}t \right\rbrack\ \ \ \ \ \ \ \ (8)\]
Where Deff is the effective moisture diffusivity (m2/s), r is the radius of the spherical sample (m), and n is the positive integer. For long drying times, equation (8) simplifies to a limiting form of the diffusion equation as follows:
\[MR = \frac{6}{\pi^{2}}\exp\left( - \frac{{\pi^{2}D}_{eff}}{4r^{2}}t \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9)\]
Plotting of ln (MR) versus drying time is expressed with the dimensionless Fourier number F0 according to equation (10).
\[\ \ \ln{MR} = - \ln\frac{\pi^{2}}{6} - \frac{\pi^{2}}{4}F_{0}\ with\ F_{0}\ = \frac{D_{eff}}{r^{2}}t\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (10)\ \ \ \ \]
Or
\[F_{0}\ = 0.4053\ln(MR) + 0.2017\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (11)\ \ \ \ \]
Activation energy
Effective diffusivity can be linked to air temperature by Arrhenius type expression (Doymaz et al., 2023), such as:
\[D_{eff} = D_{0}\exp\left\lbrack - \frac{E_{a}}{R(T + 273.15)} \right\rbrack\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (12)\]
Where D0 is the constant of the Arrhenius type equation (m2/s), Ea is the activation energy (J/mol), T is the uniform temperature of the sweet potato (°C) and R=8, 3145 is the universal gas constant (J/mol K). Equation (12) can be rearranged into the form:
\[\ln\left( D_{eff} \right) = \ln\left( D_{0} \right) - \ \frac{E_{a}}{R(T + 273.15)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13)\]
Statistical analysis
Four statistical parameters were used to determine the ability of the tested model to represent the experimental data, namely: the coefficient of determination (R2), the root mean square error (RMSE), the reduced chi-square (χ2) and the sum of squared errors (SSE):
\[R^{2} = 1 - \frac{\sum_{i = 1}^{N}\left( P_{exp,i} - P_{pre,i} \right)^{2}}{\sum_{i = 1}^{N}\left( {\overline{P}}_{\exp} - P_{exp,i} \right)^{2}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (14)\]
\[RMSE = \left\lbrack \frac{\sum_{i = 1}^{N}\left( P_{exp,i} - P_{pre,i} \right)^{2}}{N} \right\rbrack^{\frac{1}{2}}\ \ \ \ \ \ \ (15)\]
\[\chi^{2} = \frac{\sum_{i = 1}^{N}\left( P_{exp,i} - p_{pre,i} \right)^{2}}{N - z}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (16)\]
\[SSE = \sum_{i = 1}^{N}\left( P_{exp,i} - P_{pre,i} \right)^{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (17)\]
Where P is the hot air drying parameter, Pexp,I is the experimental value of the parameter, Ppre,I is the value of the parameter P predicted by the statistical model, P̅exp,I is the average value of the parameter P, N is the number of experimental observations and z is the number of constant coefficients in the model regression. A good fit of the drying model is found for the highest values of R2 and for the lowest values of RMSE, χ2 and SSE (Compaoré et al., 2022).
Conclusion
Drying of sweet potato sphere samples was carried out at air temperatures of 50°C, 60°C, 70°C and 80°C using 2 and 3 cm diameter samples to study the influence of process variables including air temperature and sample diameter on drying characteristics including moisture ratio, mean effective moisture diffusivity and activation energy. In experiments, changes in moisture content recorded during drying time were converted to moisture ratio values and used to explain the influence of drying process variables on drying characteristics of sweet potato spheres. Moisture contents were influenced by sample diameters and hot air-drying temperatures. Increasing the air temperature and sample diameter resulted in a reduction in the drying time for the temperature influence and an increase in the drying time for the diameter influence. The effective moisture diffusivity decreased relatively with increasing moisture ratio value at all warm air temperatures. A polynomial of degree five was derived to correlate the effective moisture diffusivity with the moisture ratios of sweet potato spheres. The average effective moisture diffusivity increased as the air temperature and the diameter of the spherical sweet potato samples increased. The air temperature dependence of the average effective moisture diffusivity values was described by an Arrhenius-type equation. This dependence allowed the determination of the activation energy values of spherical sweet potato. The activation energy values increase by 30.50 and 27.71 kJ/mol when the sample diameter varies from 2 to 3 cm. Our results of the influence of process variables could contribute to obtaining better quality of dried spherical sweet potatoes. They could also serve as input data for simulation of industrial sweet potato drying systems.
Acknowledgement
The authors thank the research teams of the laboratory of materials of Helio-physics and environment of the Nazi BONI University for data acquisition.
References
Abano EE, Ma H, Qu J (2011) Influence of air temperature on the drying kinetics and quality of tomato slices. J Food Process Technol. 02(05). https://doi.org/10.4172/2157-7110.1000123
Adie GE, Inyang UE (2024) Response surface methodology for the optimization of sweet potatoes (Ipomoea batatas) drying process conditions. J Mod Technol Eng. 9(1): 16‑24. https://doi.org/10.62476/jmte9116
Amagloh FC, Yada B, Tumuhimbise GA, Amagloh FK, Kaaya AN (2021) The potential of sweet potato as a functional food in sub-saharan Africa and its implications for health: A Review. Molecules. 26(10) : Article 10. https://doi.org/10.3390/molecules26102971
Anabel F, Celia R, Germán M, Rosa R (2018) Determination of effective moisture diffusivity and thermodynamic properties variation of regional wastes under different atmospheres. Case Stud Therm Eng. 12, 248‑257. https://doi.org/10.1016/j.csite.2018.04.015
Antal T (2023) Influence of two-stage drying methods on the physical properties and drying characteristics of sweet potato slices. Food Res. 1‑17. https://doi.org/10/1/FR-2023-348.pdf
Arebo MA, Feyisa JD, Tafa KD, Satheesh N (2023) Optimization of spray-drying parameter for production of better quality orange fleshed sweet potato (Ipomoea batatas L.) powder: Selected physiochemical, morphological, and structural properties. Heliyon. 9(1): e13078. https://doi.org/10.1016/j.heliyon.2023.e13078
Ayonga EO, Ondieki DM, Ronoh EK (2023) Effects of different pretreatments on thin-layer drying kinetics, vitamin A retention and rehydration of orange-fleshed sweet potato slices. J Agric Sci Technol. 22(6): Article 6. https://doi.org/10.4314/jagst.v22i6.2
Badiora OA, Morakinyo TA, Taiwo KA (2023) Some quality properties of yellow-fleshed sweet potato flour as affected by different drying methods. Food Prod Process Nutr. 5(1): 21. https://doi.org/10.1186/s43014-023-00136-1
Bebartta JP, Sahoo NR, Dash SK, Panda MK, Pal US (2014) Kinetics modeling and moisture diffusivity of onion slices in fluidized bed drying: Fluidized bed drying of onion shreds. J Food Process Preserv. 38(1): 193–199. https://doi.org/10.1111/j.1745-4549.2012.00764.x
Compaoré A, Ouoba S, Ouoba KH, Simo-Tagne M, Rogaume Y, Ahouannou C, Dissa AO, Béré A, Koulidiati J (2022) A modeling study for moisture diffusivities and moisture transfer coefficients in drying of “Violet de Galmi” onion drying. Adv Chem Eng Sci. 12(3): Article 3. https://doi.org/10.4236/aces.2022.123013
Darvishi H, Najafi G, Hosainpour A, Khodaei J, Aazdbakht M (2013) Far-infrared drying characteristics of mushroom slices. Chem Prod Process Model. 8(2): 107–117. https://doi.org/10.1515/cppm-2013-0035
Dinrifo RR (2012) Effects of pre-treatments on drying kinetics of sweet potato slices. Agric Eng Int CIGR J. 14(3): Article 3.
Domínguez-Pérez LA, Concepción-Brindis I, Lagunes-Gálvez LM, Barajas-Fernández J, Márquez-Rocha FJ, García-Alamilla P (2019) Kinetic studies and moisture diffusivity during cocoa bean roasting. Processes. 7(10): Article 10. https://doi.org/10.3390/pr7100770
Doymaz İ, Tunçkal C, Göksel Z (2023) Comparison of drying kinetics, energy efficiency and color of dried eggplant slices with two different configurations of a heat pump dryer. Energy Sources Part Recovery Util Environ Eff. 45(1): 690–707. https://doi.org/10.1080/15567036.2023.2169415
Edeani NJ, Anyaene HI (2023) Optimization of hot air drying of sweet potato using response surface method. Int J Adv Sci Eng. 10(2): 3362–3371. https://doi.org/10.29294/IJASE.10.2.2023.3362-3371
Ertekin C, Firat MZ (2017) A comprehensive review of thin-layer drying models used in agricultural products. Crit Rev Food Sci Nutr. 57(4): 701–717. https://doi.org/10.1080/10408398.2014.910493
Fan K, Chen L, He J, Yan F (2015) Characterization of thin layer hot air drying of sweet potatoes (Ipomoea batatas L.) slices. J Food Process Preserv. 39(6): 1361–1371. https://doi.org/10.1111/jfpp.12355
Gazor HR, Minaei S (2005) Influence of temperature and air velocity on drying time and quality parameters of pistachio (Pistacia vera L.). Dry Technol. 23(12): 2463–2475. https://doi.org/10.1080/07373930500341708
Igbozulike AO, Ndirika VIO, Simonyan KJ (2023) Influence of drying process variables on the effective moisture diffusivity and activation energy of African oil bean seed. Sci Afr. 22: e01895. https://doi.org/10.1016/j.sciaf.2023.e01895
Jahanbakhshi A, Kaveh M, Taghinezhad E, Rasooli Sharabiani V (2020) Assessment of kinetics, effective moisture diffusivity, specific energy consumption, shrinkage, and color in the pistachio kernel drying process in microwave drying with ultrasonic pretreatment. J Food Process Preserv. 44(6): e14449. https://doi.org/10.1111/jfpp.14449
Jiang N, Ma J, Ma R, Zhang Y, Chen P, Ren M, Wang C (2022) Effect of slice thickness and hot-air temperature on the kinetics of hot-air drying of crabapple slices. Food Sci Technol. 43: e100422. https://doi.org/10.1590/fst.100422
Junqueira JRJ, Correa JLG, Petri I, Gatti IP, de MKS (2022) Microwave drying of sweet potato: Drying kinetics and energetic analysis. J Crop Sci. 16(10): 1185–1192. https://doi.org/10.3316/informit.887929944308919
Kamble MG, Singh A, Kumar N, Dhenge RV, Rinaldi M, Chinchkar AV (2022) Semi-empirical mathematical modeling, energy and exergy analysis, and textural characteristics of convectively dried plantain banana slices. Foods. 11(18): Article 18. https://doi.org/10.3390/foods11182825
Obregon FIV, Silvano MBC, Vicencio JG, Pestaño LDB (2020) Numerical simulation of the drying kinetics of sweet potato to prevent the growth of the fungi Rhizopus oryzae. IOP Conf Ser Mater Sci Eng. 778(1): 012076. https://doi.org/10.1088/1757-899X/778/1/012076
Olawale AS, Omole SO (2012) Thin layer drying models for sweet potato in tray dryer. Agric Eng Int CIGR J. 14(2): Article 2.
Onwude DI, Hashim N, Abdan K, Janius R, Chen G (2019) The effectiveness of combined infrared and hot-air drying strategies for sweet potato. J Food Eng. 241: 75‑87. https://doi.org/10.1016/j.jfoodeng.2018.08.008
Onwude DI, Hashim N, Janius RB, Nawi NM, Abdan K (2016) Modeling the thin-layer drying of fruits and vegetables: A review. Compr Rev Food Sci Food Saf. 15(3): 599‑618. https://doi.org/10.1111/1541-4337.12196
Ouoba KH, Ganame A-S, Zougmore F (2021) Research of the characteristic dimension of the transfers during the convective drying of the sweet potato for the parallelepipedic and spherical shapes. Adv Mater Phys Chem. 11(12): 267‑276. https://doi.org/10.4236/ampc.2021.1112022
Pinheiro MNC, Castro LMMN (2023) Effective moisture diffusivity prediction in two Portuguese fruit cultivars (Bravo de Esmolfe apple and Madeira banana) using drying kinetics data. Heliyon. 9(7). https://doi.org/10.1016/j.heliyon.2023.e17741
Rezende LV, Paraizo WB, Santos JDA, Amorim KA, Goulart GAS, Becker FS, Damiani C (2024) Study of the drying process of the purple-fleshed sweet potato (Ipomoea batatas (L.) Lam) in spouted bed. Food Sci Technol. 44. https://doi.org/10.5327/fst.00180
Royen MJ, Noori AW, Haydary J (2020) Experimental study and mathematical modeling of convective thin-layer drying of apple slices. Processes. 8(12): Article 12. https://doi.org/10.3390/pr8121562
Sakouvogui A, Barry TA, Sakho AM, Keita M (2023) Experimentation of a forced convection solar dryer for drying sweet potatoes at the Higher Institute of Technology of Mamou-Guinea. World J Eng Technol. 11(3): Article 3. https://doi.org/10.4236/wjet.2023.113038
Shamala S, Fouda T (2023) Behaviour of sweet potato moisture content in a hybrid drying system. Sci Pap Ser Manag Econ Eng Agric Rural Dev. 23(1). https://managementjournal.usamv.ro/pdf/vol.23_1/Art73.pdf
Singh NJ, Pandey RK (2012) Convective air drying characteristics of sweet potato cube (Ipomoea batatas L.). Food Bioprod Process. 90(2): 317‑322. https://doi.org/10.1016/j.fbp.2011.06.006
Souza DG, Resende O, Moura LC, Ferreira WN, Andrade JWS (2019) Drying kinetics of the sliced pulp of biofortified sweet potato (Ipomoea batatas L.). Eng Agríc. 39: 176‑181. https://doi.org/10.1590/1809-4430-Eng.Agric.v39n2p176-181/2019
Süfer Ö, Sezer S, Demir H (2017) Thin layer mathematical modeling of convective, vacuum and microwave drying of intact and brined onion slices. J Food Process Preserv. 41(6): e13239. https://doi.org/10.1111/jfpp.13239
Thao HM, Noomhorm A (2011) Modeling and effects of various drying methods on sweet potato starch properties. Walailak J Sci Technol WJST. 8(2): Article 2.
Torki-Harchegani M, Ghasemi-Varnamkhasti M, Ghanbarian D, Sadeghi M, Tohidi M (2016) Dehydration characteristics and mathematical modelling of lemon slices drying undergoing oven treatment. Heat Mass Transf. 52(2): 281‑289. https://doi.org/10.1007/s00231-015-1546-y
Tüfekçi S, Özkal SG (2023) The optimization of hybrid (microwave–conventional) drying of sweet potato using response surface methodology (RSM). Foods. 12(16): Article 16. https://doi.org/10.3390/foods12163003
Wang C, Lu Y, An X, Tian S (2022) Thin-layer drying characteristics of Easter lily (Lilium longiflorum Thunb.) scales and mathematical modeling. Food Sci Technol. 42: e23222. https://doi.org/10.1590/fst.23222
List of symbols
| d | Diameter of the product (m) |
|---|---|
| d.b. | dry basis |
| D0 | Constant of Arrhenius type (m2 s-1) |
| Deff | Effective moisture diffusivity (m2 s-1) |
| Deff,ave | Average effective moisture diffusivity (m2 s-1) |
| DR | Drying rate (kgwater/(kgdry mass s)) |
| dt | Infinitesimal time (s) |
| F0 | Fourier number (-) |
| Ea | Activation energy (J mol-1) |
| m(t) | mass of wet product (kg) |
| min | minute (min) |
| ms | Dry mass (kg) |
| MR | Moisture ratio (-) |
| n | Positive integer (-) |
| r | Radius (m) |
| R | Universal gas constant = 8314.46 J mol-1 K-1 |
| R2 | Coefficient of determination (-) |
| RMSE | Root-Mean-Square error (-) |
| SSE | Sum of squared error (-) |
| t | Tim (s) |
| T | Air Temperature (°C or K) |
| X0 | Initial mean moisture content (kgwater/kgdry mass) |
| Xe | Equilibrium moisture content (kgwater/kgdry mass) |
| X (t) | Moisture content (kg water/kgdry mass) |
| χ2 | Chi-square reduced (-) |